FOCUSR: Feature-Oriented Correspondence Using Spectral Regularization

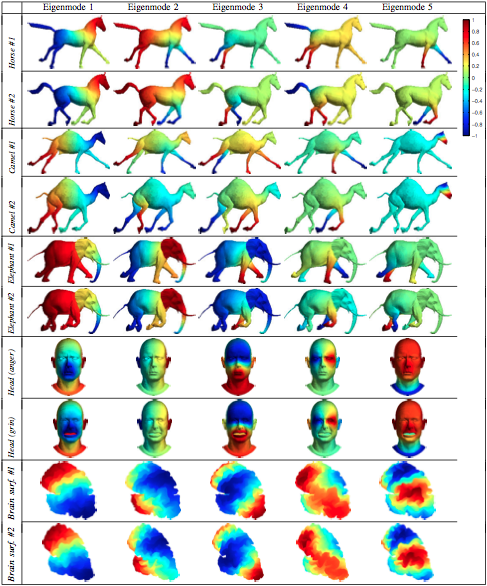
FOCUSR [1,2] is novel algorithm for dense vertex correspondence between two surface meshes. It benefits from the speed of direct matching of features over a surface and uses spectral correspondence as a mean of regularization. Spectral methods have been used for shape matching by comparing the lowest-frequency (smooth) eigenvectors of a graph Laplacian (representing inherent geometric properties of the mesh surfaces, see Fig. 1). FOCUSR takes advantage of the smoothness of these lowest-frequency eigenvectors to regularize an embedding containing any set of extra features (e.g., metrics derived from the mesh, or external measures).

Spectral Correspondence

Figure: Two frames from a sequence of a galloping animals, head poses, and two human brain surfaces. Each row shows the first five spectral components (eigenmodes) of a model, given by the eigendecomposition of the graph Laplacian of the model (eigenvectors have been reordered and their sign adjusted, so both sets correspond). The color scale indicates the value of the spectral coordinate over the surface.

Adjacency Matrix - Edge Weighting

Eigenvectors of the graph Laplacian of a mesh represent inherent geometric properties of this surface. For $n$ vertices, let $W$ be the weighted adjacency matrix describing the connections between the vertices. Given a distance metric $\mathrm{dist}(i,j)$ between points $i$ and $j$ :

$$W_{ij} = \begin{cases}1 / \mathrm{(dist)}(i,j) \mathrm{if} \exists\; e_{ij} \in \mathscr{E}, 0 \;\;\;\;\;\;\;\mathrm{otherwise} \end{cases}$$ (1)

The distance metric can be based on the distance between vertices: $\mathrm{dist}(i,j) = \Vert\mathbf{x}_i - \mathbf{x}_j\Vert$ , or if additional features $\mathbf{F}$ are used (e.g., surface curvatures, mesh texture, virtually any extra measurements):

$$\mathrm{dist}(i,j) =\left\Vert (\mathbf{x}_i, \gamma \mathbf{F}_i) - (\mathbf{x}_j, \gamma \mathbf{F}_j) \right\Vert,$$ (2)

where $(\mathbf{x}, \gamma\mathbf{F})$ is the concatenation of the 3D coordinate values $\mathbf{x} = (x,y,z)^{\mbox{\tiny T}}$ with the $K$ feature values $\mathbf{F} = (\mathbf{f}^{(1)},\dots,\mathbf{f}^{(K)})^{\mbox{\tiny T}}$ , while $\gamma$ is a weighting parameter for each feature.

Graph Laplacian - Node Weighting

The general Laplacian operator is formulated as the $n \times n$ matrix with the form:

$$L = G \left(D - W\right),$$ (3)

where $D$ is the degree matrix (diagonal matrix with $D_{ii} = \sum_j W_{ij}$ ), and $G$ is the diagonal matrix of node weights. Typically in spectral correspondence $G$ is set to identity $G = \mathrm{Id}\hspace{.5ex}$ , or to $G = D^{-1}$ . However, it is proposed to set $G$ as any meaningful node weighting (e.g., positive feature magnitudes):

$$w_i = G_{ii} = \frac{1}{d_i} \cdot \frac{1}{\displaystyle\sum_{k=1}^K \gamma_i \rho\left(f_i^{(k)}\right)},$$ (4)

where $d_i$ is the node degree (i.e., $D_{ii}$ ), $\gamma$ is the previously mentioned feature weights, and $\rho(\cdot)$ is a function that enforces positive values (e.g., $\rho(f) = f^2$ or $\rho(f) = \exp(f)$ ). The denominator in Eq. (5) contains the sum of the influences of each feature on vertex $v_i$ . We used $\rho(f) = \exp\left(f\right)$ to promote correspondence between nodes having the largest feature components (which we assume indicate greatest significance).

$$G_{ii} = \frac{1}{D_{ii}} \cdot \frac{1}{\displaystyle\sum_{k=1}^K \gamma_i \rho\left(f_i^{(k)}\right)},$$ (5)

where $D_{ii}$ is the node degree, $\gamma$ the previously mentioned feature weights, and $\rho(\cdot)$ a function that enforces positive values on node weights (e.g., $\rho(f) = f^2$ or $\rho(f) = \exp(f)$ ).

Spectral Coordinates

The right eigenvectors of the Laplacian matrix $L$ comprise the graph spectrum $\mathbf{\mathcal{X}} = ( \mathbf{x}^{(1)},$ $\mathbf{x}^{(2)},$ $\dots,$ $\mathbf{x}^{(n)})^{\mbox{\tiny T}}$ . The values over surfaces for the five lowest frequency eigenvectors are shown on Fig. 1, and illustrates the stability of these eigenvectors between articulated or highly deformable shapes. here, $\mathbf{x}$ represents the 3D coordinate in space (i.e., $x,y,z$ ), and the superscripted $\mathbf{x}^{(i)}$ represents the $i^$th spectral coordinate (i.e., the $i^$th eigenvector of the graph Laplacian. Each eigenvector $\mathbf{x}^{(u)}$ is a column matrix with $n$ values, and represents a different (weighted) harmonic on a mesh surface that corresponds to an inherent property of the mesh geometry. The $n$ values $( x_i^{(1)},$ $x_i^{(2)},$ $\dots,$ $x_i^{(n)})$ give the spectral coordinates of node $v_i$ (i.e., a coordinate in a spectral domain).

The first eigenvector $\mathbf{x}^{(1)}$ is the trivial (uniform) eigenvector, and the eigenvectors associated with the lower non-zero eigenvalues (e.g., $\mathbf{x}^{(2)}, \mathbf{x}^{(3)}$ ) represent coarse (i.e., low-frequency) intrinsic geometric properties of the shape. The first of them $\mathbf{x}^{(2)}$ is called the Fiedler vector, while eigenvectors associated with higher eigenvalues (e.g., $\mathbf{x}^{(n-1)}, \mathbf{x}^{(n)}$ ) represent fine (high-frequency) geometric properties. For example, in Fig. 1, the values of $\mathbf{x}^{(2)}$ increase along a virtual centerline depicting the global shape of the models (a coarse intrinsic property), while the values of $\mathbf{x}^{(5)}$ depict finer details of the models.

Spectral Ordering

Only the first $M$ lowest-frequency eigenvectors ( $\mathcal{X}^M$ and $\mathcal{Y}^M$ ) are of interest. In practice, these eigenvectors on both meshes needs to be reordered (their sign might be flipped, and due to algebraic multiplicity, eigenvectors of close eigenvalues might be swapped). Reordering is done by checking the values of these eigenvectors between pairs of closest points on the mesh surface ( $y_{\mu(i)}$ on mesh $Y$ is the closest point of $x_i$ on mesh $X$ ). The matrix $C$ gathers all dissimilarities between eigenvector $x^{(u)}$ and $y^{(v})$ :

$$C(u,v) = \sum_{i=1}^N \left(x^{(u)}_i - y^{(v)}_{\mu(i)} \right)^2.$$

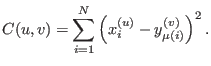The Hungarian algorithm can find the optimal permutation $\pi$ so each eigenvector $x^{(u)}$ corresponds with $y^{(\pi(u))}$ .

Embedding Regularization

Initial feature vectors $F_x$ and $F_y$ are extended with the reordered eigenvectors $\mathcal{X}^M$ and $\mathcal{Y}^M$ to form an extended spectral embedding:

$$\mathbf{X} = (c_x \mathbf{\mathcal{X}}^M, \beta \mathbf{F}_x),$$ (6)

$$\mathbf{Y} = (c_y \mathbf{\mathcal{Y}}^M, \beta \mathbf{F}_y),$$ (7)

where $c_x,c_y$ are weighting parameters based on the eigenvector frequencies and their reordering confidence, and $\beta$ a weghting parameter for each feature (e.g., $\beta=\gamma$ of Eq. (2) ).

These spectral embeddings are regularized using a non rigid point set correspondence. Coherent Point Drift (CPD) is used [1].

Spectral Matching

The extended spectral embeddings have been regularized with the smoothness of their spectral components. Closest points between these aligned embeddings reveal corresponding points between both meshes. The correspondence map can be further regularized in space in order to respect the spatial neighborhood of the meshes. The final correspondence map is given such that:

$$\mathbf{X} = \phi(\mathbf{Y})$$ (8)

Results

FOCUSR works on regular meshes when using its simplest setting (no additional features are required). Below, the illustration shows that finding closest points in space faces the challenge of working directly in the spatial domain, while the correspondences become clearer in the spectral domain. FOCUSR uses a different approach as it takes advantage of the smoothness of the lowest harmonics to regularize matching.

Figure: Direct matching (coloring indicates correspondence, and links and circles indicate matching of leg extremities, crosses indicate ground truth) : (a) Finding closest points in space (i.e., match $X$ with $Y$ ). (b) Finding closest points in the spectral domain (i.e., match embedding $\mathcal {X}$ with $\mathcal {Y}$ instead of mesh $X$ with $Y$ ). Even though the meshes are not aligned in space (they are translated), their spectral embeddings (red $\mathcal {X}$ , blue $\mathcal {Y}$ in 3D) are almost perfectly superimposed. FOCUSR in its simplest setting : (c) Our method performs matching in the spectral domain (with lower error over the surface) and improves the alignment of the spectral embeddings. Note that no additional features are used here in FOCUSR.

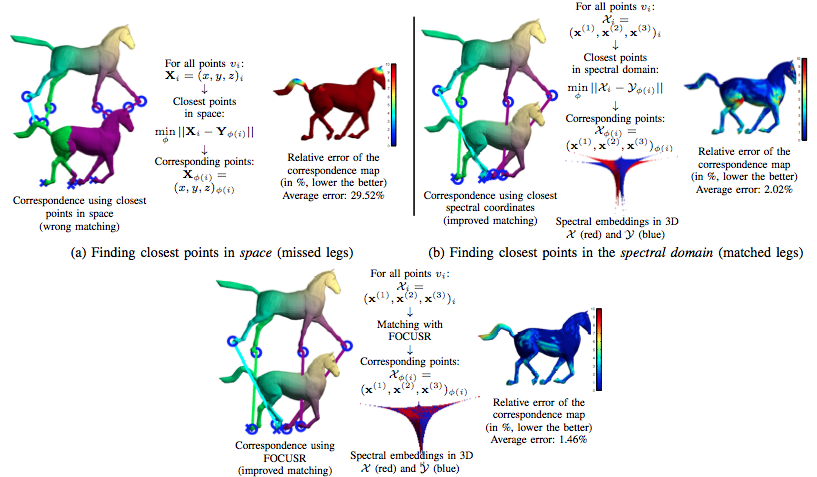
FOCUSR can match meshes undergoing important non rigid transformations and articulated meshes. Below are examples of galloping animals and of different facial expressions.

Figure: Correspondences across animated sequences for a horse gallop (average error of 1.41% ($\pm$ 0.57%), a camel gallop 1.42% ($\pm$ 0.65%), an elephant gallop 0.95% ($\pm$ 0.54%), and facial expression changes 0.47% ($\pm$ 0.26%). Corresponding points have a unique color across each sequence. Note that no temporal consistency was enforced (each frame was matched independently with the first frame). Blue circles show corresponding points along the sequences found with FOCUSR. Blue crosses show the true corresponding points.

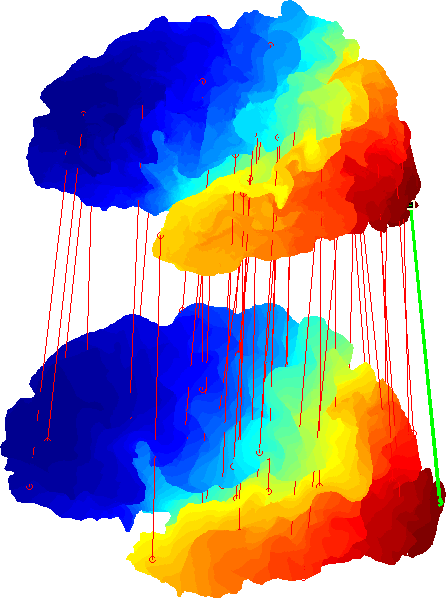
FOCUSR can also be used for precise and accurate correspondence in medical imaging. Below is a matching between two cerebral cortices which are highly convoluted surfaces. FOCUSR matches the accuracy of state-of-the-art brain matching algorithm with the benefit of being inherently extremely fast.

Figure 5: Illustrating pairs of corresponding nodes (red links) between two cortices. The mesh coloring is the magnitude of the Fiedler vector. The correspondence is found by identifying closest nodes in the spectral representations.

Code

CODE IS UNDER REVISION AND AVAILABLE IN ITS CURRENT FORM FOR REVIEW ONLY

http://step.polymtl.ca/~rv101/spectral-correspondence.zip

Bibliography

1

Lombaert, H.; Grady, L.; Polimeni, J. R. and Cheriet, F. FOCUSR: Feature Oriented Correspondence using Spectral Regularization - A Method for Precise Surface Matching. PAMI, 2013.

2

Lombaert, H.; Grady, L.; Polimeni, J. R. and Cheriet, F. Fast Brain Matching with Spectral Correspondence. IPMI, 2005.

1

Myronenko, A. and Song, X. Point-set registration: Coherent point drift. PAMI, 2010.